Viés de confusão

Publicado por 30 de Agosto de 2023 em Estudantes para Melhores Evidências

Definição 

O viés de confusão é o viés que ocorre quando uma variável relacionada com o desfecho do estudo e/ou com a exposição é mensurada ou considerada de modo inadequado na análise, levando a uma associação falsa ou distorcida (superestimando ou subestimando a associação) [1]. 

Pode ocorre em estudos observacionais (coortes e estudos caso-controle) ou experimentais (ensaios clínicos randomizados), porém, ocorre mais frequentemente nos estudos observacionais, pois a ausência de randomização torna os grupos comparados desbalanceados em relação a características na linha de base [2]. 

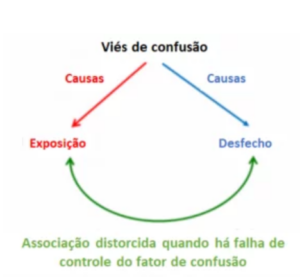
Figura 1. O princípio do viés de confusão. O confundidor torna a exposição mais provável, e de alguma forma e de modo independente, modifica o desfecho, fazendo parecer que há uma associação entre a exposição e o desfecho quando não há; ou mascarando uma associação verdadeira (Fonte: https://oxfordbrazilebm.com/index.php/vies-de-confusao/ com autorização dos tradutores) [3].   

Exemplos de fatores de confusão 

Quadro 1 apresenta alguns exemplos de viés de confusão. 

Quadro 1. Exemplos de viés de confusão [1,4,5]

Como prevenir ou minimizar os fatores de confusão 

Controlar os fatores de confusão é um aspecto importante no planejamento e condução de um estudo para minimizar erros de associação entre desfecho e a intervenção.  

Preferencialmente os possíveis confundidores devem ser identificados na fase de planejamento (com métodos adequados de métodos de randomização, restrição, pareamento e subgrupos) e, quando isso não é possível, as medidas devem ser adotadas no momento de análise (com a adoção de ajustes estatísticos). 

(1) Randomização 

A atribuição randômica dos indivíduos entre os grupos de intervenção / exposição e os grupos de controle será útil para minimizar tanto fatores de confusão conhecidos quanto os desconhecidos e, devido a isso, é indispensável em um bom desenho de estudo. Quando dois grupos são randomicamente selecionados, há uma distribuição semelhante de diversos fatores que podem se comportar como fatores de confusão. Em um estudo devidamente randomizado, cada participante do estudo terá uma chance igual de ser alocado em qualquer um dos grupos e por conseguinte, em teoria, cada grupo terá uma porcentagem igual de homens, uma porcentagem igual de pessoas com excesso de peso, um número igual de mulheres com unhas pintadas de vermelho e assim por diante, melhorando, assim, a distribuição equivalente de possíveis fatores confundidores entre os dois grupos. Aqui vale também ressaltar que quanto maior é o tamanho da amostra melhor é a distribuição equivalente de fatores entre os grupos [5]. 

(2) Restrição 

Restringir a população de um estudo, com critérios de inclusão e exclusão bem definidos e justificados, também pode ajudar a reduzir os riscos de confusão já que exclui do desenho do estudo indivíduos que tenham sido expostos a fatores de confusão conhecidos e irá controlar a confusão causada por essas variáveis. Por exemplo, em um estudo investigando se há associação entre abuso do álcool e incidência de câncer de fígado, independentemente de tabagismo, os investigadores poderiam restringir a população de estudo aos não fumantes utilizando o tabagismo como critério de exclusão do estudo. 

 (3) Pareamento 

O pareamento é uma outra forma de minimizar os fatores de confusão muito utilizado em estudos de caso-controle, fazendo com que os grupos sejam igualmente distribuídos entre os grupos de intervenção / exposição e grupo controle. São selecionados, nesse caso, participantes com características semelhantes para compor os dois grupos. Por exemplo, em um estudo publicado em 2012, Driver et al. realizaram um estudo de controle de caso avaliando a relação entre demência e câncer subsequente. Eles parearam cada caso de demência com até três controles do mesmo sexo e idade, que eram livres de demência no momento do diagnóstico de demência do caso [6]. 

 (4) Análises de subgrupos 

Podemos analisar os resultados de um estudo de forma separada para diferentes subgrupos (estratos) da amostra total. Separamos esses subgrupos por meio da seleção de diferentes fatores de confusão, como por exemplo, por idade ou por sexo, fazendo, assim, a análise de resultados separada para cada subgrupo. É importante ressaltar que quanto maior a estratificação em subgrupos menor é o tamanho da amostra para cada subgrupo, diminuindo assim o poder estatístico de análise do estudo. 

 (5) Ajustes estatísticos 

Os ajustes estatísticos nos ajudam a corrigir os efeitos causados pelos fatores confundidores durante nossa análise de resultados. Nesse método, um modelo estatístico pode ser construído para ajustar a medida de efeito de uma intervenção para diversos fatores confundidores que muitas vezes coexistem (p. ex., a razão de risco calculada em um estudo de controle de caso investigando uma associação entre ingerir bebidas carbonatadas ricas em aspartame e a doença de Parkinson pode ser ajustada para idade, classe social, tabagismo e sexo). Calcular a medida “ajustada” de associação entre uma exposição e a doença (por meio da avaliação de fatores de confusão simultaneamente) é um modelo de ambiente natural melhor do um modelo estatístico que tenta controlar e analisar cada fator de confusão individualmente, já que a exposição, a doença e fatores de confusão coexistem na população real [5]. 

 Conclusão 

A randomização é a melhor estratégia para reduzir o risco de viés de confusão. No entanto, ela pode não ser suficiente, particularmente quando se prevê que desequilíbrios nos fatores prognósticos podem ocorrer após a randomização, ou quando desequilíbrios ocorrem por acaso. Nesses casos, estratificação e ajustes estatísticos podem reduzir o risco de viés de confusão.

Autores: Jonas Paulo Silva de Menezes, Lucca Sokabe, Mateus Menezes dos Santos, Matheus Rodrigues Almeida, Palloma Souza Marques Dourado e Victor Henrique Cardinali Barros. 

Citar como: Menezes JPS, Sokabe L, Santos MM, Almeida MR, Dourado PSM, Barros VHC. Viés de confusão. Estudantes para Melhores Evidências. Cochrane. Disponível em: [adicionar link da página da web]. Acessado em: [adicionar dia, mês e ano de acesso]. 

Referências 

1. Lorraine K. Alexander, Brettania Lopes, Ricchetti-Masterson K,  Yeatts KB. Confounding Bias, Part I. Eric Notebook: Disponível em: https://sph.unc.edu/wp-content/uploads/sites/112/2015/07/nciph_ERIC11.pdf. Acessado em 14 de agosto 2023. 
2. Catalogue of bias collaboration, Aronson JK, Bankhead C, Nunan D. Confounding. In Catalogue Of Biases. 2018. Disponível em: https://catalogofbias.org/biases/confounding/. Acessado em 14 de agosto 2023. 
3. Viés de confusão. Disponível em: https://oxfordbrazilebm.com/index.php/vies-de-confusao/. Acessado em 14 de agosto 2023. 
4. Celentano DD, Szklo M (2019). More on causal inference: Bias, confounding, and interaction. In Celentano DD, Szklo M. Gordis epidemiology. (pp. 289-306). doi://dx.doi.org/10.1016/B978-0-323-55229-5.00015-2. Disponível em:  https://www.clinicalkey.es/#!/content/3-s2.0-B9780323552295000152. Acessado em 14 de agosto 2023. 
5. Jonathan AC Sterne, Miguel A Hernán, Alexandra McAleenan, Barnaby C Reeves, Julian PT Higgins. Assessing risk of bias in a non-randomized study. Disponível em: https://training.cochrane.org/handbook/current/chapter-25#_Ref534457886. cessado em 14 de agosto 2023. 
6. Driver JA, Beiser A, Au R, Kreger BE, Splansky GL, Kurth T, Kiel DP, Lu KP, Seshadri S, Wolf PA. Inverse association between cancer and Alzheimer’s disease: results from the Framingham Heart Study. BMJ. 2012;344:e1442. doi: 10.1136/bmj.e1442. PMID: 22411920; PMCID: PMC3647385. 

Tags: